October 4, 2006
(Revised October 27, 2006)
Consider a delay differential equation (DDE) of the form
dx/dt
= F[x(t), x(t-T)]
where T is a constant delay time. This equation is infinite-dimensional in the sense that a continuum of initial conditions over the interval -T < t < 0 is required to specify the behavior. For typical nonlinear functions F, analytic solutions are impossible especially in the case where the dynamics are chaotic, and hence numerical methods must be used. Such methods entail approximating the continuous evolution of x by an iterative mapping at discrete (but small) time steps. There is no unique way to do this, but perhaps the simplest is the Euler method
where T is a constant delay time. This equation is infinite-dimensional in the sense that a continuum of initial conditions over the interval -T < t < 0 is required to specify the behavior. For typical nonlinear functions F, analytic solutions are impossible especially in the case where the dynamics are chaotic, and hence numerical methods must be used. Such methods entail approximating the continuous evolution of x by an iterative mapping at discrete (but small) time steps. There is no unique way to do this, but perhaps the simplest is the Euler method
x(t+h) = x(t)
+ hF[x(t),
x(t-Nh)]
where h is the (small) time step and N = T/h is one minus the dimension of the iterated map, which can be equivalently expressed in the form
where h is the (small) time step and N = T/h is one minus the dimension of the iterated map, which can be equivalently expressed in the form
x0(t+h) = x0(t) + TF[x0(t),
xN(t)]/N
xi(t+h) = xi-1(t) for 1 < i < N
Dividing the last term in first equation above by (N + 1/2) rather than by N gives a slightly better result, but that was not done here. An alternate representation is in terms of N + 1 ordinary differential equations (ODEs)
xi(t+h) = xi-1(t) for 1 < i < N
Dividing the last term in first equation above by (N + 1/2) rather than by N gives a slightly better result, but that was not done here. An alternate representation is in terms of N + 1 ordinary differential equations (ODEs)
dx0/dt = F(x0,
xN)
dxi/dt = N(xi-1 - xi+1)/2T for 1 < i < N - 1
dxN/dt = N(xN-1 - xN)/T
which can be solved by any of the standard methods such as Runge-Kutta.
Consider now the special case of the Mackey-Glass equation, which is a prototypical delay differential equation:
dxi/dt = N(xi-1 - xi+1)/2T for 1 < i < N - 1
dxN/dt = N(xN-1 - xN)/T
which can be solved by any of the standard methods such as Runge-Kutta.
Consider now the special case of the Mackey-Glass equation, which is a prototypical delay differential equation:
dx/dt
= ax(t-T)/(1+x(t-T)c)
- bx(t)
with typical parameters of a = 0.2, b = 0.1, c = 10, and T = 23 that give chaos. The following table gives the results:
These values are to be compared with the value of LLE = 0.00956 + 0.00005 given by Grassberger and Procaccia in Physica D 13, 34-54 (1984) using a more accurate map with N = 600 described in Physica D 9, 189-208 (1983).
For a second comparison, consider the Ikeda delay differential equation:
The following table gives the results:
PowerBASIC code for calculating the entire spectrum of Lyapunov exponents for this system is available along with an executable version which gives the following results for N = 100:
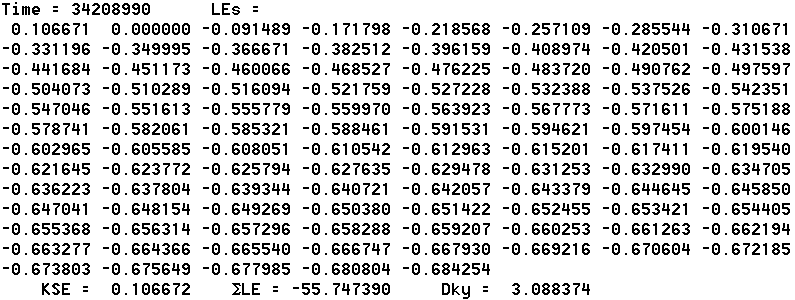
with typical parameters of a = 0.2, b = 0.1, c = 10, and T = 23 that give chaos. The following table gives the results:
| N |
LLE (iterated
map) pb source & exe file |
LLE (ODE) pb source & exe file |
| 10 |
0.00973 |
0.00806 |
| 100 |
0.00961 |
0.00936 |
| 1000 |
0.00939 |
0.00943 |
| 10000 |
0.00947 |
converges too slowly |
These values are to be compared with the value of LLE = 0.00956 + 0.00005 given by Grassberger and Procaccia in Physica D 13, 34-54 (1984) using a more accurate map with N = 600 described in Physica D 9, 189-208 (1983).
For a second comparison, consider the Ikeda delay differential equation:
dx/dt
= asin2[x(t-T)
- c] - bx(t)
with typical parameters of a = 20, b = 1, c = pi/4, and T = 5 that give chaos. The following table gives the results:
These values are to be compared with the value of LLE = 0.2078 given by Vicente, Dauden, Colet, and Toral in IEEE Journal of Quantum Electronics 41, 541-548 (2005).
Source code in C++ for calculating the entire spectrum of Lyapunov exponents by the Wolf algorithm for the Ikeda DDE using the Euler method is available from Kostas Chlouverakis. A PowerBASIC translation is also available along with an executable version.
For a final comparison, consider the elegant variant of the Ikeda delay differential equation
with typical parameters of a = 20, b = 1, c = pi/4, and T = 5 that give chaos. The following table gives the results:
| N |
LLE (iterated map) | LLE (ODE) |
| 10 |
0.3573 |
0.2415 |
| 100 |
0.2042 |
0.2457 |
| 1000 |
0.2075 |
0.2103 |
| 10000 |
0.2077 |
converges too slowly |
These values are to be compared with the value of LLE = 0.2078 given by Vicente, Dauden, Colet, and Toral in IEEE Journal of Quantum Electronics 41, 541-548 (2005).
Source code in C++ for calculating the entire spectrum of Lyapunov exponents by the Wolf algorithm for the Ikeda DDE using the Euler method is available from Kostas Chlouverakis. A PowerBASIC translation is also available along with an executable version.
For a final comparison, consider the elegant variant of the Ikeda delay differential equation
dx/dt
= sin x(t-2pi)
The following table gives the results:
| N |
LLE (iterated map) | LLE (ODE) |
| 10 |
0.1012 |
0 |
| 100 |
0.1068 |
0.1067 |
| 1000 |
0.1067 |
0.1066 |
| 10000 |
converges too slowly |
PowerBASIC code for calculating the entire spectrum of Lyapunov exponents for this system is available along with an executable version which gives the following results for N = 100:
