Contact

News!

Books

Home

Calculus and Pizza
A Math Cookbook for the Hungry Mind

Clifford A. Pickover

John Wiley & Sons, 2003



Order from Amazon.com.
"Taking mathematics from the beginning of the world
to the time of Newton, what he has
done is much the better half."
-- Gottfried Wilhelm Leibniz, co-discoverer of calculus

"If I have seen further than others,
it is by standing upon the shoulders of giants."
 -- Isaac Newton, the other discoverer of calculus

"If I have not seen as far as others,
it is because giants were standing on my shoulders."
 -- Hal Abelson, MIT Professor


Delicious fast food for the mind that makes learning calculus as easy as eating a slice
Click here to see the book at Amazon.Com!


"Non-cooks think it's silly to invest two hours' work in two minutes' enjoyment; but if cooking is evanescent, well, so is the ballet." -- Julia Child, US chef, author, TV hostess

If you obtain this book, you will hold a special book in your hands. Sure, there are plenty of other excellent Introductory calculus books for sale. But I have found that none of them have all the features of Calculus and Pizza. Let's consider a few trends: "It's fun to get together and have something good to eat at least once a day. That's what human life is all about -- enjoying things." -- Julia Child

Impress Friends! Expand Your Mind!

The mysterious, quirky, and fun puzzles in this book should cause even the most left-brained readers to fall in love with calculus. The antics of Luigi, Fiona, Rosario, and Big Tony will entertain people at all levels of mathematical sophistication. In fact, this book focuses on creativity, discovery, and challenge.

When chef Luigi talks to students about the problems in this book, the students are always fascinated to learn that is possible for them to solve seemingly complicated real-world problems and make new discoveries with just a pencil and paper. The students are surprised to learn that calculus has affected every field of scientific endeavor and plays invaluable roles in fields ranging from science to sociology, from modeling ecological disasters and the spread of diseases to understanding the architecture of our brains The pepperoni and pizza problems are metaphors for the amazing range of calculus applications.

"Pizza is a lot like calculus. Except the limit is how much you can eat." -- Luigi

One of the abiding sins of mathematicians is an obsession with completeness -- an urge to go back to first principles to explain their works. As a result, readers must often wade through pages of background before getting to the essential ingredients. To avoid this burden, each chapter in this book is short. You'll quickly get the essence of a technique or question. A number of the basic methods and challenges are representative of a wider class of problems of interest to mathematicians today. One advantage of this brief format is that you can jump right in to experiment and have fun, without having to sort through a lot of detritus. Thus, this book is not intended for mathematicians looking for formal mathematical explanations. Of course, this approach has some disadvantages. In just a few pages, Luigi can't go into any depth on a subject. You won't find much historical context, philosophy, or extended discussions. You won't find proofs and derivations; I simply present most of the important formulas. The focus is on procedures and drills for solving problems and not on some of the deeper meanings of calculus.

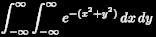I became interested in calculus early in childhood when gazing at a book in my father's dusty study. The book contained multiple integrals like . These strange symbols impressed the heck out of me. I wondered if I would I ever be able to understand what an integral was. My father's books provided a seed from which my interest in calculus grew, and, along with my love of pizza, provided an early stimulus for Calculus and Pizza.

"The only real stumbling block is the fear of failure. In cooking, you've got to have a what-the-hell attitude." -- Julia Child

Calculus and Pizza is for anyone who has pondered what calculus is all about, for students who want to do well on exams and get into good colleges or graduate schools, and for lay people who want to get just a taste or a refresher course. The book might most effectively be used as a supplement to a traditional calculus text. If you've not taken calculus for a few years, then Calculus and Pizza can serve as a quick review of some of the essential rules, formulas, and problems. I assume that the reader is familiar with high school algebra and some of the basic rules of trigonometry.

I hope that Calculus and Pizza will stimulate creative thinking, get some students interested in computer programming, and suggest the usefulness of simple mathematics for solving curious, practical, or even mind-shattering problems. The ability of our future workforce to meet our needs for mathematicians, scientists, and engineers depends on the education today's children receive. Recent statistics indicate that America is in grave danger of failing to meet the challenge. For much of the 1990s, U. S. students ranked low on scores in science and math in comparison to other countries. I hope Calculus and Pizza is first in a series of books that make complex topics in science and math a bit more fun while emphasizing basic and practical principles.

"Today, calculus has invaded every field of scientific endeavor and plays invaluable roles in biology, physics, chemistry, economics, sociology, engineering -- and in any field where some quantity, like speed or temperature, changes. Calculus can be used to help explain the structure of a rainbow, teach us how to make more money in the stock market, guide a spacecraft, make weather forecasts, predict population growth, design buildings, quantify happiness, and analyze the spread of AIDS. Calculus has caused a revolution. It has changed the way we look at the world." -- Cliff Pickover


Clifford A. Pickover received his Ph.D. from Yale University and is the author of thirty highly-acclaimed books on such topics as computers, art, religion, mathematics, black holes, human intelligence, time travel, and alien life. His web site, Pickover.com, has received over a million visits.

Table of Contents

Preface
Introduction
1. Pizza Velocity and the Derivative
2. Derivative Definitions and Rules
3. Derivatives and Slopes	
4. Rules for Products and Quotients
5. Chain Rule and Implicit Differentiation
6. Maxima and Minima
7. Min Max Pizza Applications
8. Exponentials and Logarithms
9. Limits and Continuity
10. Related Rates
11. Integration
12. Logarithmic Differentiation, Integration by Parts, Trigonometric Substitution, 
	and Partial Fractions
13. Exponential Growth and Decay
14. Calculus and Computers
15. Multiple Integrals
16. Calculus in  a Nutshell
17. Luigi's Mind-Boggling Workout Routine

Conclusion
Answers to Odd-Numbered Exercises
Further Reading

Index

The index will give you more ideas about some of the topics covered. 
Abelson, Hal, vii
answers to problems, 157-204
antiderivatives, 93-94, 101, 104
applications (of calculus) 6-7, 12, 138-139
area, and integrals, 97
area between two curves, 99
Barrow, Isaac, xiii
base changes, 58
Berkeley, George, xii
Bolyai, Janos, xiv
Burton, David, xi
calculus
  applications of, 6-7, 12, 138-139
  first use of symbols, xiv, 13
  first textbook on, xiv
  fundamental anagram of, 155
  fundamental theorem of, 97
  history of, xii-xiv
chain rule, 25-34
  exponential, 62
  logarithmic, 62
  trigonometric, 29-30
Child, Julia, xi, 1
computers
  calculus and, 127-134
  programs, 69-70, 129, 132

concavity, 41-43
concave up and down, 42
conclusion, 155-156
continuity, 65-79
  definition, 73, 75
cosine rules, 29-30
critical points, 37-39, 47
Darwin, Charles, xiv
decay, exponential, 119-126
decreasing functions, 36
definite integrals, 95, 105
derivatives, xiii, 3-7, see also chain rule
  definitions, 9-14, 128
  first use of symbol, xiv, 13
  rules, 9-14, 21-34, 58
  slopes, 17-20, 36
  velocity, 3-7
Descartes, Rene, xiii
differential equations, 121
differentiablity, of functions, 77
differentiation, see also derivatives
  logarithmic, 107-109
e (Euler's number), 59-61
exercises, additional, 151-153
exponential rule, 62
exponential growth and decay, 119-126
exponentials, 57-64
extended power rule, 27
fluxions, xii, 156
formulas, summary of, 141-149
fractal, 74-74
functions, increasing and decreasing, 36
fundamental theorem of calculus, 97
God's formula, 61
growth, exponential, 119-126
history of calculus, xii-xiv
implicit differentiation, 30-34, 82
increasing functions, 36
indefinite integrals, 95, 101, 104
indeterminate form, 71
infinitesimals, xiv, 13
inflection points, 37-40
integrals
  area, 97
  definite, 95, 101, 104
  definition of, 95
  first use of symbol, xiv
  indefinite, 95, 101, 104
  multiple, 135-139
integration, xii, xiv, 93-106
  by parts, 110-111
  partial fractions, 114-116
  Riemann, 97
  rules, 99, 101
  trigonometric substitution, 111-112
intervals, 47-48, 53
Kammerer, Paul, xiv
Koch curve, 74-75, 76
Leibniz, Gottfried, vii, xiii-xiv, 13, 155-156
L'Hôpital's rule, 71-74
limits, 10, 18, 65-79, 128
local minima and maxima, 37-39, 47-48
logarithm rules, 58, 62
logarithmic differentiation, 107-109
logarithms, 57-64
maxima and minima, 35-44, 47-48
   local, 37-39, 47-48
menu, calculus, 66
min-max applications, 45-55
multiple integrals, 135-139
multiplier rule, 10
Newton, Isaac, vii, xiii-xiv, 13, 155-156
partial fractions, 114-116
parts (integration by), 110-111
power rule, 10, 27
  extended, 27
product rule, 21-24
quotient rule, 21-24
ranges, 48
related rates, 81-91
Riemann integrals, 97
rule summary, 141-149
second derivative test, 38-39
sine rules, 29-30
slopes (and derivatives), 17-20, 36
sum rule, 10
summary of formulas, 141-149
tangent lines, 18, 36
trigonometric chain rules, 29-30
trigonometric derivatives, 29-30
trigonometric substitution, 111-112
velocity, 3-7
Wallis, John,xiii
workout routine, 151-155