Contact |
News! |
Books |
Home |
Contact |
News! |
Books |
Home |
 The humble sine waves that lie at the very foundation of
trigonometry have a special beauty all their own. It takes just a
little coddling to bring the beauty out. But who would guess, for
example, that psychedelic fractal patterns lurk within the cosine
operation applied to real numbers?
The humble sine waves that lie at the very foundation of
trigonometry have a special beauty all their own. It takes just a
little coddling to bring the beauty out. But who would guess, for
example, that psychedelic fractal patterns lurk within the cosine
operation applied to real numbers?
Consider the union of the infinite set of curves produced by Carotid-Kundalini functions defined by:
y = cos(n*x*acos(x))
where (-1 < x < 1, n = 1, 2, 3, ...), and "acos" designates the arccosine
function. The set of superimposed curves is very simple to plot -- most
computer hobbyists could easily program and plot them on a personal
computer -- but the curves have an extremely complicated and beautiful
structure. For example, for (x < 0 ) there appears to be an exotic
fractal structure with gaps repeated at different size scales and with
progressively increasing spacing as x becomes smaller.
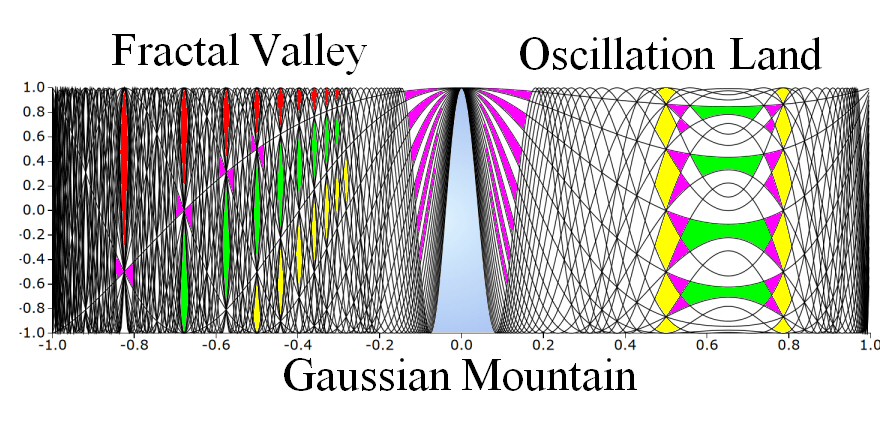
You can compute the union of the first 25 curves using the following
logic (a more complete program listing is provided at the end):
for (n=1; n < =25; n=n+1) {
for (x= -1; x < = 1; x=x+.01) {
y = cos((float)n*x*acos(x));
if (x == -1) MovePenTo(x,y);
else DrawTo(x,y);
}
}
If you have the ability to display these curves, make a plot from -1 < x < 1 and -1 < y < 1. You could spend a lifetime exploring the infinite intricacies of the resulting superimposed patterns.
C program
/* Compute Carotid-Kundalini Curves */ #include <math.h> #include <stdio.h> main() { float x,y; int n; /* Superimpose 25 curves */ for (n=1; n < =25; n=n+1) { for (x = -1; x < = 1; x = x+.01) { y=cos( (float)n * x * acos(x)); /* Write out x,y points for plotting */ printf("%f %f\n",x,y); } } }BASIC program
10 REM Compute Carotid-Kundalini Curves 20 REM Superimpose 25 curves 30 FOR N=1 TO 25 40 FOR X = -1 TO 1 STEP 0.01 50 Y=COS(N * X * ACOS(X)) 60 REM Write out x,y points for plotting 70 PRINT X, Y 80 NEXT X 90 NEXT N 100 END
 More information on the Carotid-Kundalini Universe appears in
Keys to Infinity.
More information on the Carotid-Kundalini Universe appears in
Keys to Infinity.
 Cliff would like to hear from those of you who explore
these curves in greater detail or make higher resolution plots.
Cliff would like to hear from those of you who explore
these curves in greater detail or make higher resolution plots.

 For additional very intense, psychedelic, mathematical art, click
here.
For additional very intense, psychedelic, mathematical art, click
here.
 Mathematical explorers are tourists in the Carotid-Kundalini Universe. Some favorite Carotid-Kundalini
web pages are listed here:
Mathematical explorers are tourists in the Carotid-Kundalini Universe. Some favorite Carotid-Kundalini
web pages are listed here: