This problem is certainly not for the meek...

Cliff

Centered Hexamorphic Numbers by Cliff Pickover

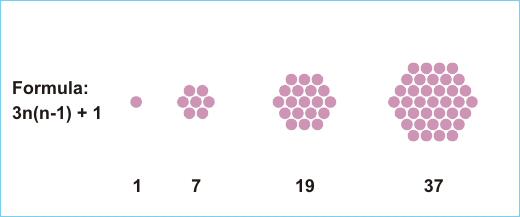Let us define centered hexagonal numbers as having the form: H = 3n(n-1)+1. They describe the number of grid points in nested concentric hexagonal lattices. A centered hexagonal number is called "centered hexamorphic" if it terminates with its associated centered hexagonal integer. For example, n = 7 is centered hexamorphic because H (7) equals 127. A convenient notation a_5 = aaaaa can be employed where the subscript indicates the number of times the digit or group appears consecutively. We note the following interesting infinite sequence: H(5 0_k 1) = 7 5 0_(k-1) 1 5 0_k 1, k = 0,1,2, .... For example, k = 2 produces H(5001) = 75015001. Can the reader find any other infinite sequences?

Wait. Don't click on the solution until you've pondered this for at least a few minutes.

Solution