Simple Models of Complex Chaotic Systems

J. C. Sprott
Department of Physics, University of Wisconsin, Madison, Wisconsin 53706

(Received 28 August 2007; accepted 8 December 2007)

ABSTRACT

Many phenomena in the real world are inherently complex and involve many dynamical variables interacting nonlinearly through feedback loops and exhibiting chaos, self-organization, and pattern formation. It is useful to ask if there are generic features of such systems, and if so, how simple can such systems be and still display these features. This paper describes several such systems that are accessible to undergraduates and might serve as useful examples of complexity.

Ref: J. C. Sprott, Am. J. Phys. 76, 474-480 (2008)

The complete paper is available in PDF format.

Return to Sprott's Books and Publications.

Fig. 1. Largest Lypunov exponent for a collection of 472 fully connected artificial neural networks in Eq. (5) with N = 101 and random Gaussian weights.
Fig. 1

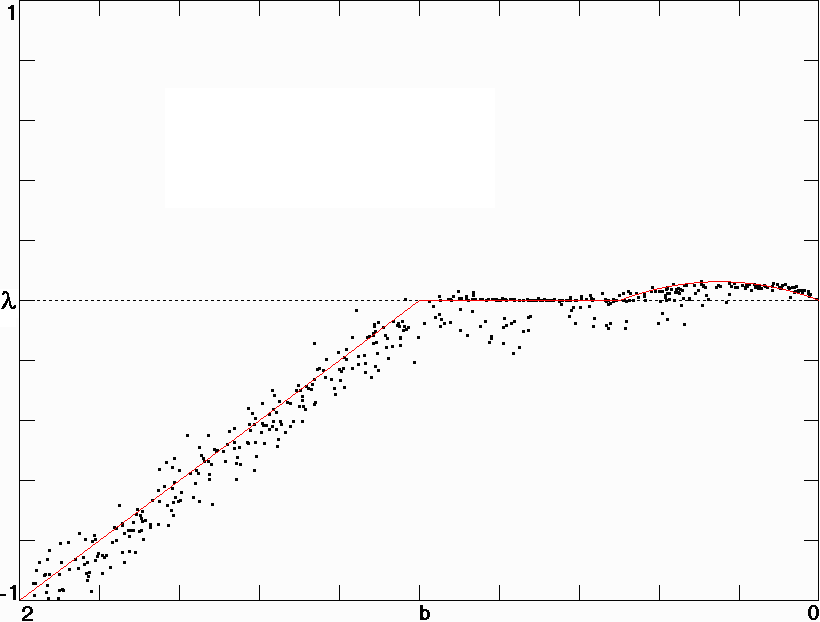
Fig. 2. Largest Lyapunov exponent for the sparse circulant neural network in Eq. (7) with N = 101 and four-neighbor interactions.
Fig. 2

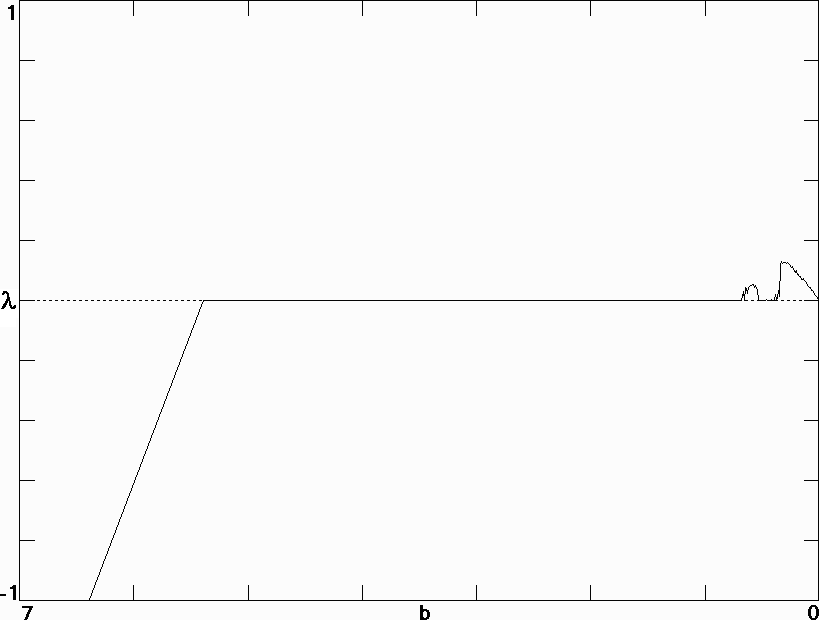
Fig. 3. Spatiotemporal plot of chaos in a sparse circulant neural network with N = 101 and b = 0.25.
Fig. 3

Fig. 4. Largest Lyapunov exponent for the hyperlabyrinth system in Eq. (8) with N = 101.
Fig. 4

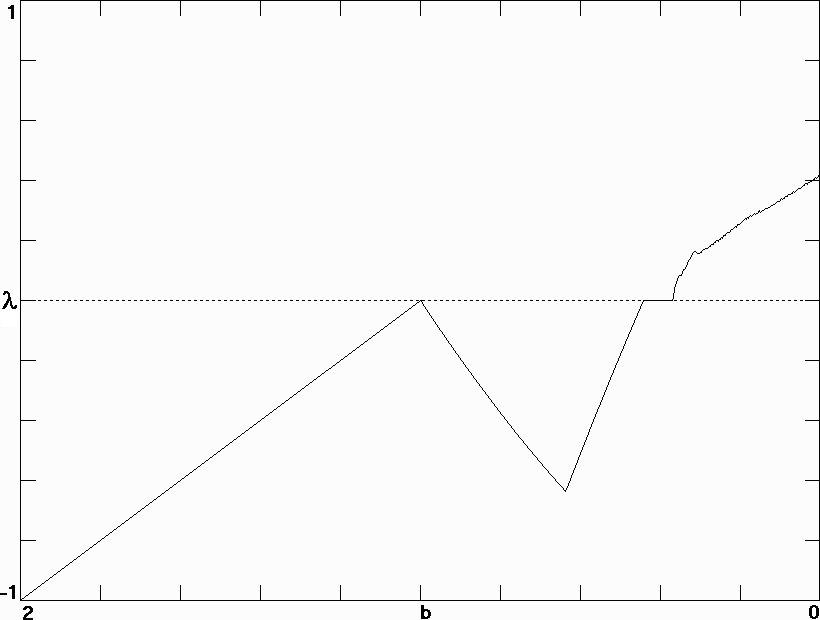
Fig. 5. Spatiotemporal plot of hyperlabyrinth chaos for N = 101 and b = 0.25.
Fig. 5

Fig. 6. Largest Lyapunov exponent for the Lotka-Volterra model in Eq. (9) with N = 101.
Fig. 6

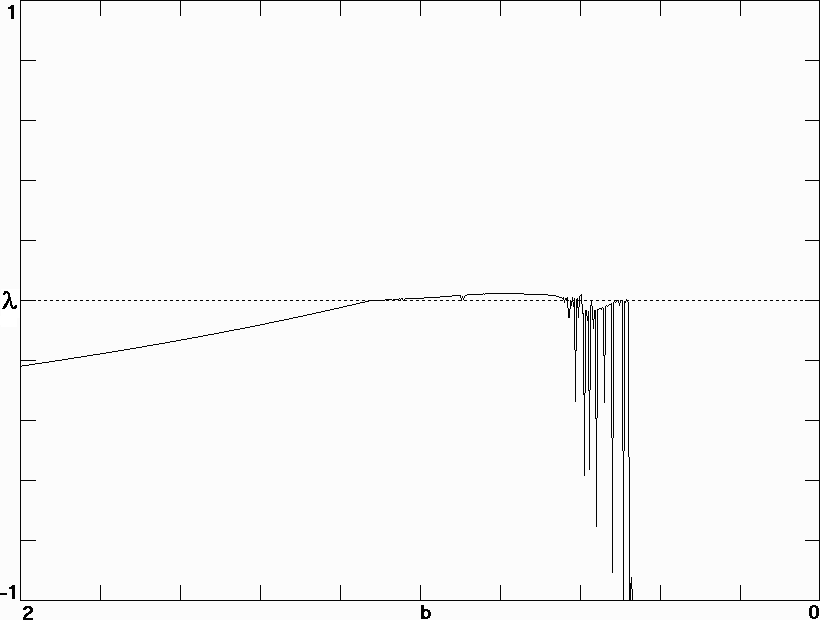
Fig. 7. Spatiotemporal plot of the Lotka-Volterra model for N = 101 and b = 0.8.
Fig. 7

Fig. 8. Largest Lyapunov exponent for the delayed differential equation model in Eq. (10) with f(x) = sin x and N = 100.
Fig. 8

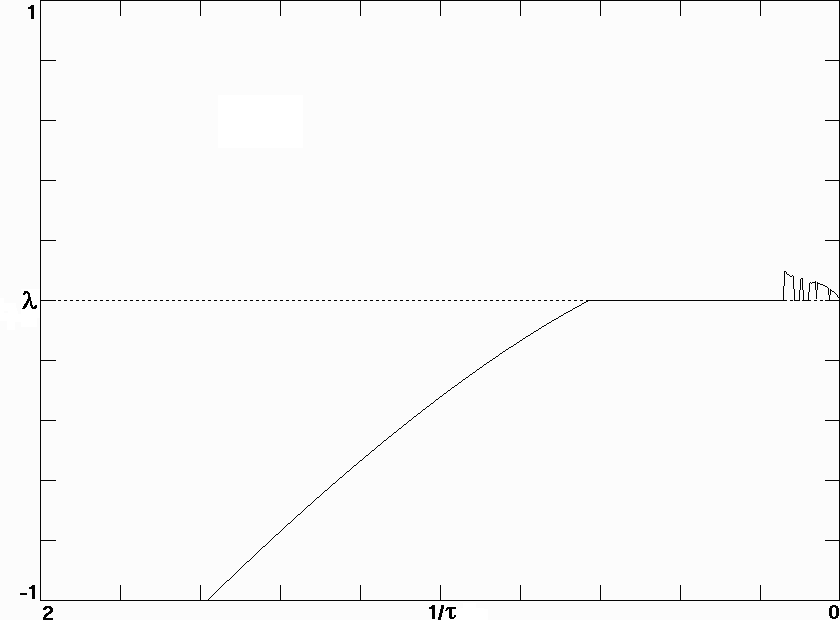
Fig. 9. Strange attractor for the delayed differ4ential equation model in Eq. (10) with f(x) = sin x, tau = 8 and N = 100.
Fig. 9

Fig. 10. Largest Lyapunov exponent for the PDE model in Eq. (13) with N = 101.
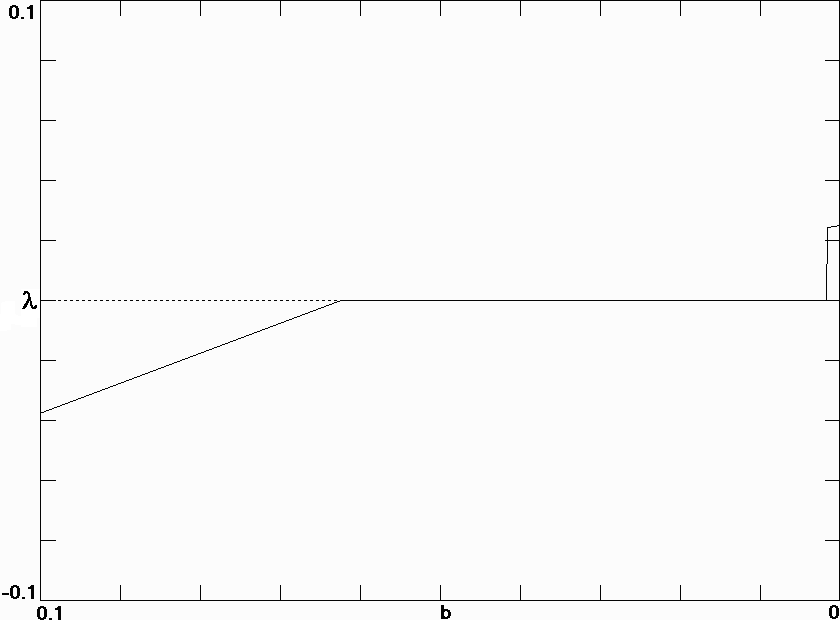
Fig. 10

Fig. 11. Spatiotemporal plot of the PDE model in Eq. (12) for N = 101 and b = 0.
Fig. 11