Lyapunov Exponents
Chaos and Time-Series Analysis
10/3/00 Lecture #5 in Physics 505
 Comments on Homework
#3 (Van der Pol Equation)
Comments on Homework
#3 (Van der Pol Equation)
-
Some people only took initial conditions inside the attractor
-
For b < 0 the attractor becomes a repellor (time reverses)
-
The driven system can give limit cycles and toruses but not chaos (?)
-
Can get chaos if you drive the dx/dt equation instead of
dy/dt
 Review (last
week) - Dynamical Systems Theory
Review (last
week) - Dynamical Systems Theory
-
Types of attractors/repellors:
-
Equilibrium points (radial, spiral, saddle) 0-D
-
Limit cycles (closed loops) 1-D
-
2-Toruses (quasiperiodic surfaces) 2-D
-
N-Toruses (hypersurfaces) N-D
-
Strange attractors (fractal) Non-integer D
(Attractor dimension < system dimension)
-
Stability of equilibrium points:
-
Find equilibrium point: f(x) = 0 ==> x*,
etc.
-
Calculate partial derivatives fx etc. at equilibrium
-
Construct the Jacobian matrix J
-
Find the characteristic equation: det(J - l)
= 0
-
Solve for the D eigenvalues: l1,
l2,
...lD
-
Find the eigenvectors (if needed) from JR = lR
-
Stable and unstable manifold (inset & outset)
-
Organize the phase space
-
Plot position of eigenvalues in complex-plane
-
If any have Re(l) > 0, point is unstable
-
Index is number of eigenvalues with Re(l)
> 0
-
Dimension of outset = index
-
Volume expansion: dV/dt / V = l1
+ l2 + l3
+ ...
-
By convention, l1 > l2
> l3 > ...
-
An attractor has dV/dt < 0
-
Different rules for stability of fixed points for maps
-
In 1-D, X = X0ln
is stable if |l| < 1
-
In 2-D and higher, stable if all l are inside
unit circle
-
Bifurcations occur when l touches unit
circle
-
Examples of chaotic dissipative flows in 3-D:
-
Driven pendulum
-
dx/dt = v
-
dv/dt = -sin x - bv + A sin wt
-
A = 0.6, b = 0.05, w = 0.7
-
Driven nonlinear oscillator (Ueda)
-
dx/dt = v
-
dv/dt = -x3 - bv + A sin
wt
-
A = 2.5, b = 0.05, w = 0.7
-
Driven Duffing oscillator
-
dx/dt = v
-
dv/dt = x - x3 - bv
+ A sin wt
-
A = 0.7, b = 0.05, w = 0.7
-
Driven Van der Pol oscillator
-
dx/dt = v
-
dv/dt = -x + b(1 - x2)v
+ A sin wt
-
A = 0.61, b = 1, w = 1.1 (a torus)
-
Can get chaos with drive in dx/dt equation
-
Lorenz attractor
-
dx/dt = p(y - x)
-
dy/dt = -xz + rx - y
-
dz/dt = xy - bz
-
p = 10, r = 28, b = 8/3
-
Rössler attractor
-
dx/dt = -y - z
-
dy/dt = x + ay
-
dz/dt = b + z(x - c)
-
a = b = 0.2, c = 5.7
-
Simplest dissipative chaotic flow
-
dx/dt = y
-
dy/dt = z
-
dz/dt = -x + y2 - Az
-
A = 2.107
-
Other simple chaotic flows
 General Properties of
Lyapunov Exponents
General Properties of
Lyapunov Exponents
-
A measure of chaos (how sensitive to initial conditions?)
-
Lyapunov exponent is a generalization of an eigenvalue
-
Average the phase-space volume expansion along trajectory
-
2-D example:
-
Circle of initial conditions evolves into an ellipse
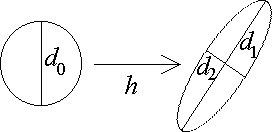
-
Area of ellipse: A = pd1d2
/ 4
-
Where d1 = d0el1t
is
the major axis
-
And d2 = d0el2t
is
the minor axis
-
Magnitude and direction continually change
-
We must average along the trajectory
-
As with eigenvalues, dA/dt / A = l1
+ l2
-
Note: l is always real (sometimes
base-2, not base-e)
-
For chaos we require l1
> 0 (at least one positive LE)
-
By convention, LEs are ordered from largest to smallest
l1 > l2 > l3 >
...
-
In general for any dimension:
-
(hyper)sphere evolves into (hyper)ellipsoid
-
One Lyapunov exponent per dimension
-
Units of Lyapunov exponent:
-
Units of l are inverse seconds for flows
-
Or inverse iterations for maps
-
Alternate units: bits/second or bits/iteration
-
Caution: False indications of chaos
-
Unbounded orbits can have l1
> 0
-
Orbits can separate but not exponentially
-
Can have transient chaos
 Lyapunov Exponent for
1-D Maps
Lyapunov Exponent for
1-D Maps
-
Suppose Xn+1 = f(Xn)
-
Consider a nearby point Xn + dXn
-
Taylor expand: dXn+1
= df/dX dXn
+ ...
-
Define el = |dXn+1/dXn|
= |df/dX| (local Lyapunov number)
-
Local Lyapunov exponent: l =
log |df/dX|
-
Can use any base such as loge (ln) or log2
-
Since df/dX is usually not constant over the orbit,
-
We average <log |df/dX|> over many iterations
-
For example, logistic map:
-
df/dX = A(1 - 2X), and
-
log |df/dX| is minus infinity at X = 1/2
-
l(A) has a complicated
shape
-
There are infinitely many negative spikes
-
A = 4 gives l = ln(2) (or 1
bit per iteration)
 Lyapunov Exponents for
2-D Maps
Lyapunov Exponents for
2-D Maps
-
Suppose Xn+1 = f(Xn,
Yn),
Yn+1
= g(Xn,
Yn)
-
Area expansion: An+1 = Anel1+l2
(as with eigenvalues)
-
l1 + l2
= <log (An+1/An)> = <log
|det J|> = <log |fxgy - fygx|>
-
For example, Hénon
map:
-
Xn+1 = 1 - CXn2
+ BYn [= f(X, Y)]
-
Yn+1 = Xn
[= g(X, Y)]
-
Alternate representation: Xn+1 =
1 - CXn2 + BXn-1
-
Note: This reduces to quadratic map for B = 0
-
Usual parameters for chaos: B = 0.3, C = 1.4
-
l1 + l2
= <log |fxgy - fygx|>
= log |-B| = -1.204 (base-e)
(or -1.737 bits per iteration in base-2)
-
Contraction is the same everywhere (unusual)
-
Numerical calculation gives l1
= 0.419 (base-e)
(or 0.605 bits per iteration in base-2)
-
Hence l2 = -1.204 - 0.419 = -1.623
(base-e)
(or -2.342 bits per iteration in base-2)
 Lyapunov Exponents for
3-D Flows
Lyapunov Exponents for
3-D Flows
-
Sum of LEs: Sl = l1
+ l2 + l3
= <trace J> = <fx + gy
+ hz>
-
Must be negative for an attractor (dissipative system)
-
This is the divergence of the flow
-
It is the fractional rate of volume expansion (or contraction)
-
For a conservative (Hamiltonian) system, sum is zero
-
For non-point attractors, one exponent must = 0
[corresponding to the direction of the flow]
-
For a chaotic system, one exponent must be positive
-
Start with any initial condition in the basin of attraction
-
Iterate until the orbit is on the attractor
-
Select (almost any) nearby point (separated by d0)
-
Advance both orbits one iteration and calculate new separation d1
-
Evaluate log |d1/d0| in any convenient
base
-
Readjust one orbit so its separation is d0 in same
direction as d1
-
Repeat steps 4-6 many times and calculate average of step 5
-
The largest Lyapunov exponent is l1
= <log |d1/d0|>
-
If map approximates an ODE, then l1
= <log |d1/d0|> / h
-
A positive value of l1 indicates
chaos

 General character
of exponents in 3-D flows:
General character
of exponents in 3-D flows:
| l1 |
l2 |
l3 |
Attractor |
| neg |
neg |
neg |
equilibrium point |
| 0 |
neg |
neg |
limit cycle |
| 0 |
0 |
neg |
2-torus |
| pos |
0 |
neg |
strange (chaotic) |
-
For flows in dimension higher than 3:
-
(0, 0, 0, -, ...) 3-torus, etc.
-
(+, +, 0, -, ...) hyperchaos, etc.
 Kaplan-Yorke (Lyapunov)
Dimension
Kaplan-Yorke (Lyapunov)
Dimension
-
Attractor dimension is a geometrical measure of complexity
-
Random noise is infinite dimensional (infinitely complex)
-
How do we calculate the dimension of an attractor? (many ways)
-
Suppose system has dimension N (hence N Lyapunov exponents)
-
Suppose the first D of these sum to zero
-
Then the attractor would have dimension D
(in D dimensions there would be neither expansion nor contraction)
-
In general, find the largest D for which l1
+ l2 + ... + lD
> 0
(The integer D is sometimes called the topological dimension)
-
The attractor dimension would be between D and D + 1
-
However, we can do better by interpolating:
DKY = D + (l1
+ l2 + ... + lD)
/ |lD+1|
-
The Kaplan-Yorke conjecture is that DKY agrees
with other methods
-
Multipoint interpolation doesn't work
-
2-D Map Example: Hénon map
(B = 0.3, C = 1.4)
-
l1 = 0.419 and l2
= -1.623
-
D = 1 and DKY = 1 + l1
/ |l2| = 1 + 0.419 / 1.623 = 1.258
-
Agrees with intuition and other calculations
-
3-D Flow Example: Lorenz Attractor (p = 10, r
= 28, b = 8/3)
-
Numerical calculation gives l1
= 0.906
-
Since it is a flow, l2 = 0
-
l1 + l2
+ l3 = <fx +
gy
+ hz> = -p - 1 - b = -13.667
-
Therefore, l3 = -14.572
-
D = 2 and DKY = 2 + l1
/ |l3| = 2 + 0.906 / 14.572 =
2.062
-
Chaotic flows always have DKY > 2
[Chaotic maps can have any dimension]
 Precautions
Precautions
-
Be sure orbit is bounded and looks chaotic
-
Be sure orbit has adequately sampled the attractor
-
Watch for contraction to zero within machine precision
-
Test with different initial conditions, step size, etc.
-
Supplement with other tests (Poincaré section, Power spectrum,
etc.)
J. C. Sprott | Physics 505
Home Page | Previous Lecture | Next
Lecture