Simple Driven Chaotic Oscillators with Complex Variables

Delmar Marshall
Department of Physics, Amrita Vishwa Vidyepeetham, Clappana 690-525, India
J. C. Sprott
Departments of Physics, University of Wisconsin, 1150 University Avenue, Madison, WI 53706, USA

(Received 12 November 2008; accepted 21 January 2009; published online 5 March 2009)

ABSTRACT

Despite a search, no chaotic driven complex-variable oscillators of the form z˙+ f(z) = eiwt or z˙+ f(z¯) = eiwt are found, where f is a polynomial with real coefficients. It is shown that, for analytic functions f(z), driven complex-variable oscillators of the form z˙+ f(z) = eiwt cannot have chaotic solutions. Seven simple driven chaotic oscillators of the form z˙+ f(z, z¯) = eiwt with polynomial f(z, z¯) are given. Their chaotic attractors are displayed, and Lyapunov spectra are calculated. Attractors for two of the cases have symmetry across the x = −y line. The systems’ behavior with w as a control parameter in the range of w = 0.1–2.0 is examined, revealing cases of period doubling, intermittency, chaotic transients, and period adding as routes to chaos. Numerous cases of coexisting attractors are also observed.

Ref: D. Marshall and J. C. Sprott, Chaos 19, 013124-1 - 013124-7 (2009)

The complete paper is available in PDF format.

Return to Sprott's Books and Publications.

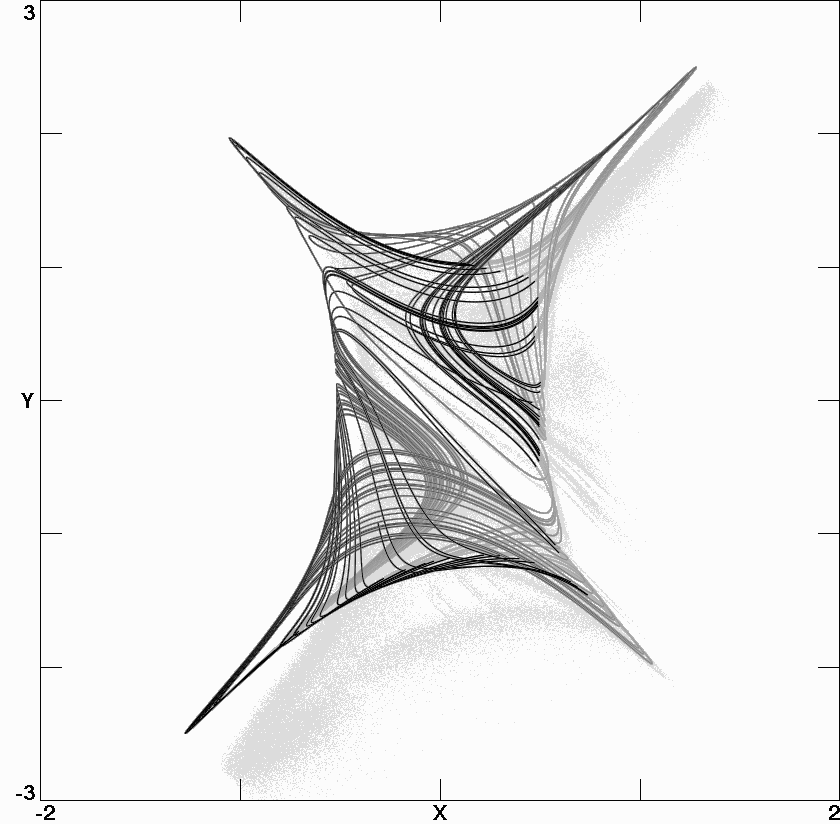
Fig. 1.
Fig. 1

Fig. 2.
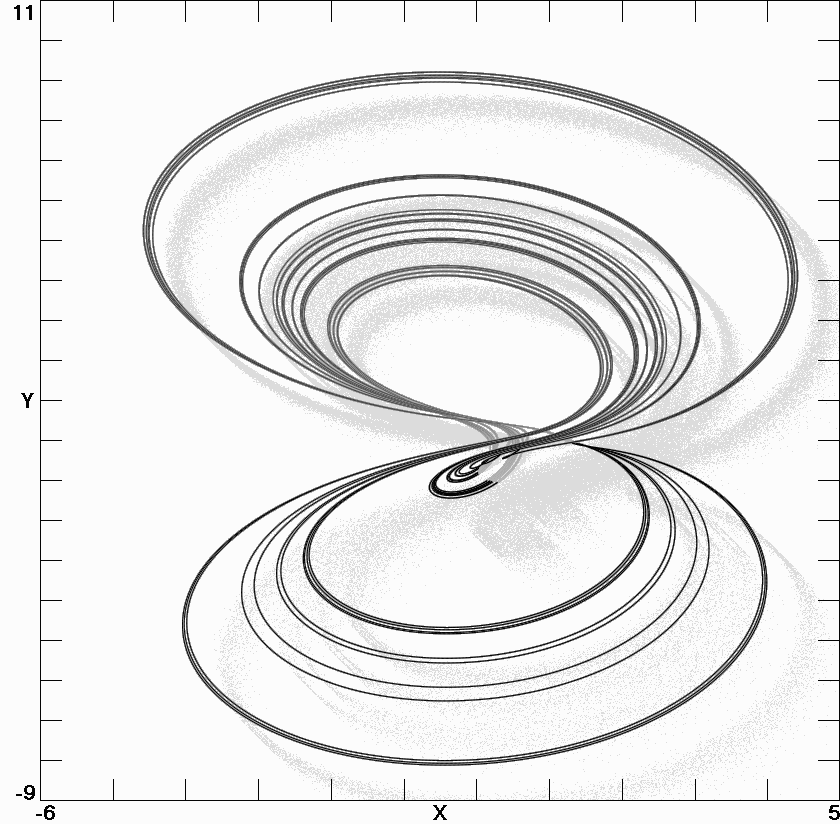
Fig. 2

Fig. 3.
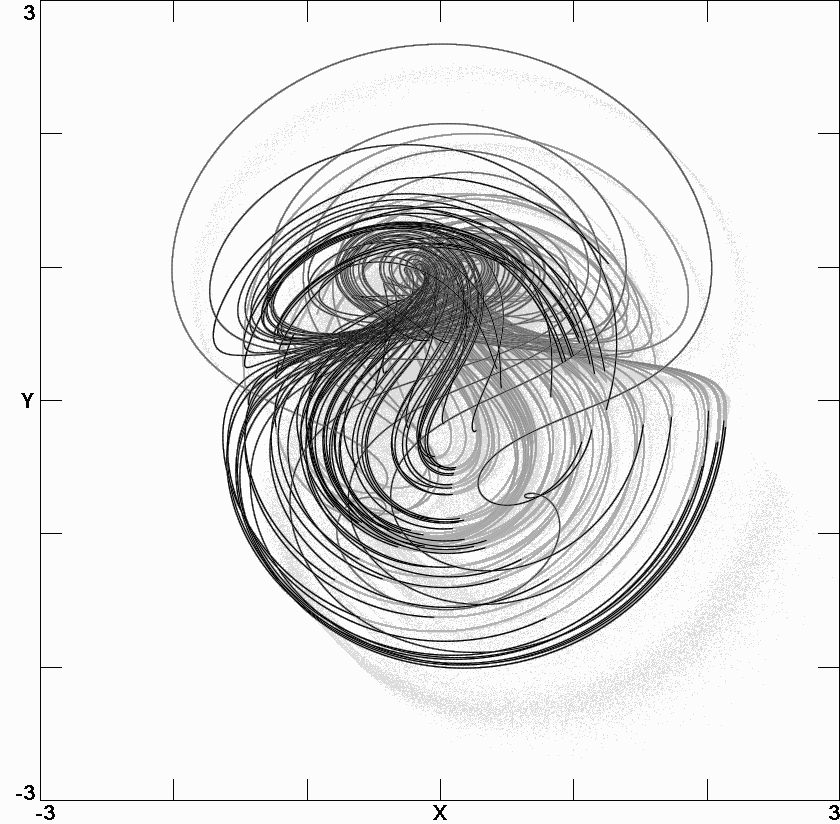
Fig. 3

Fig. 4.
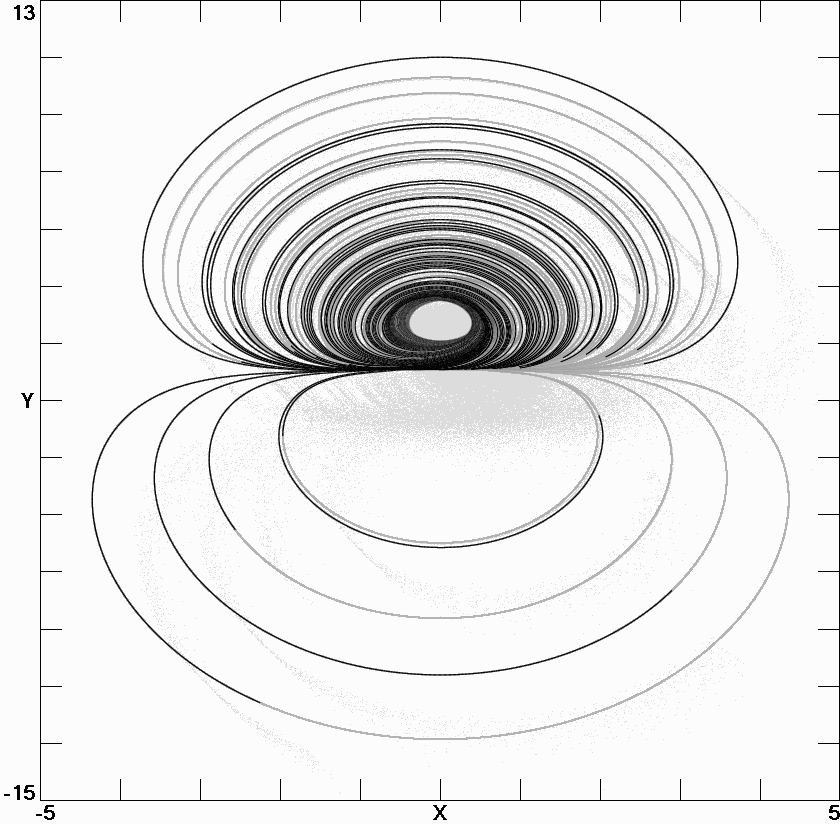
Fig. 4

Fig. 5.
Fig. 5

Fig. 6.
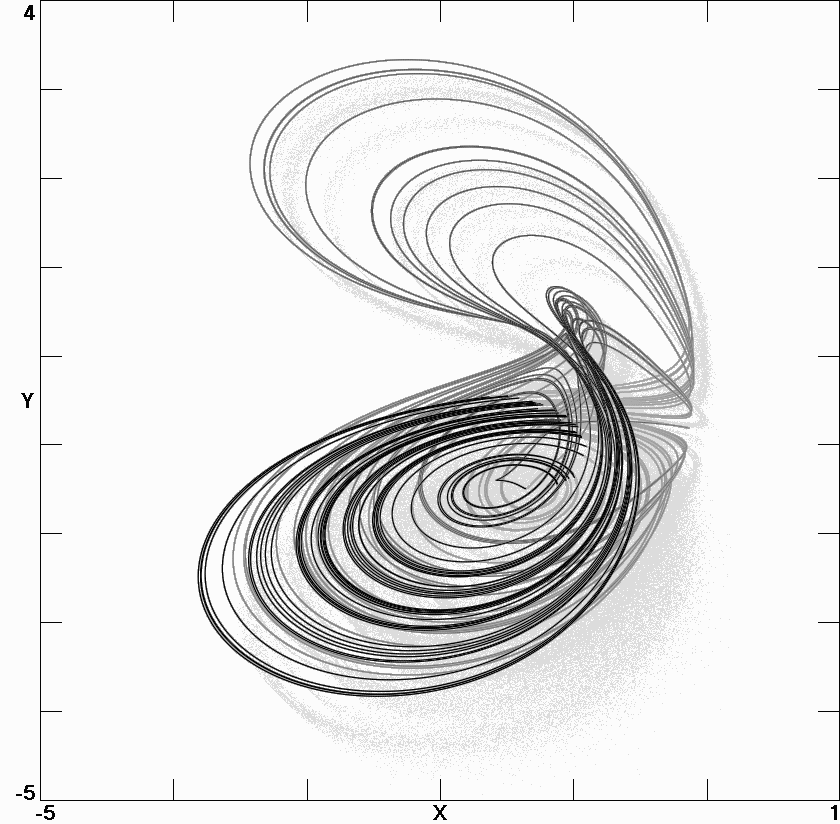
Fig. 6

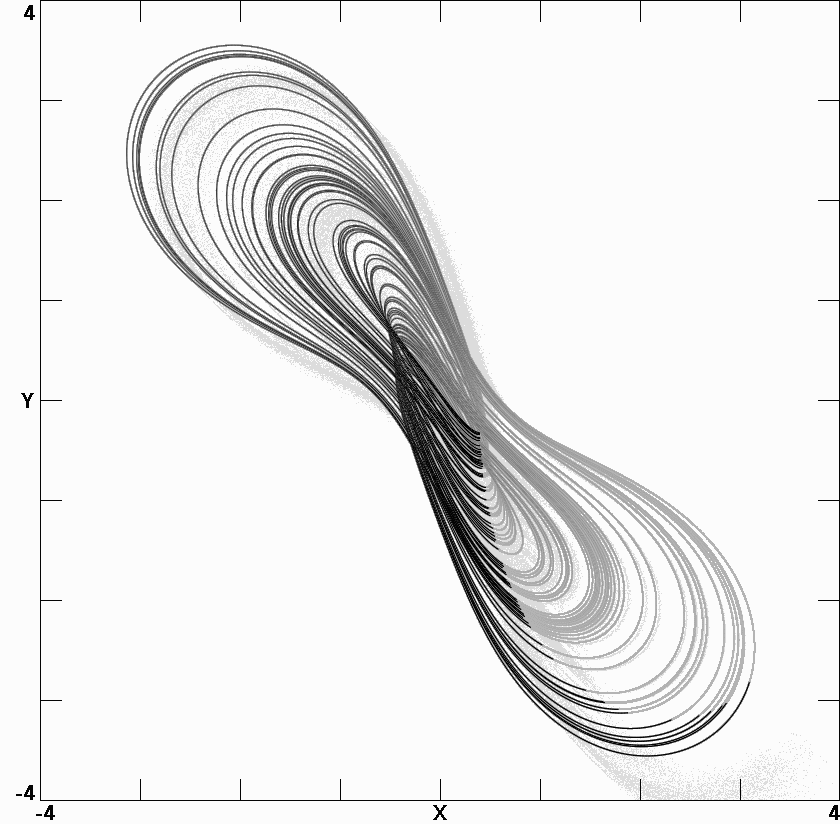
Fig. 7.
Fig. 7

Fig. 8.
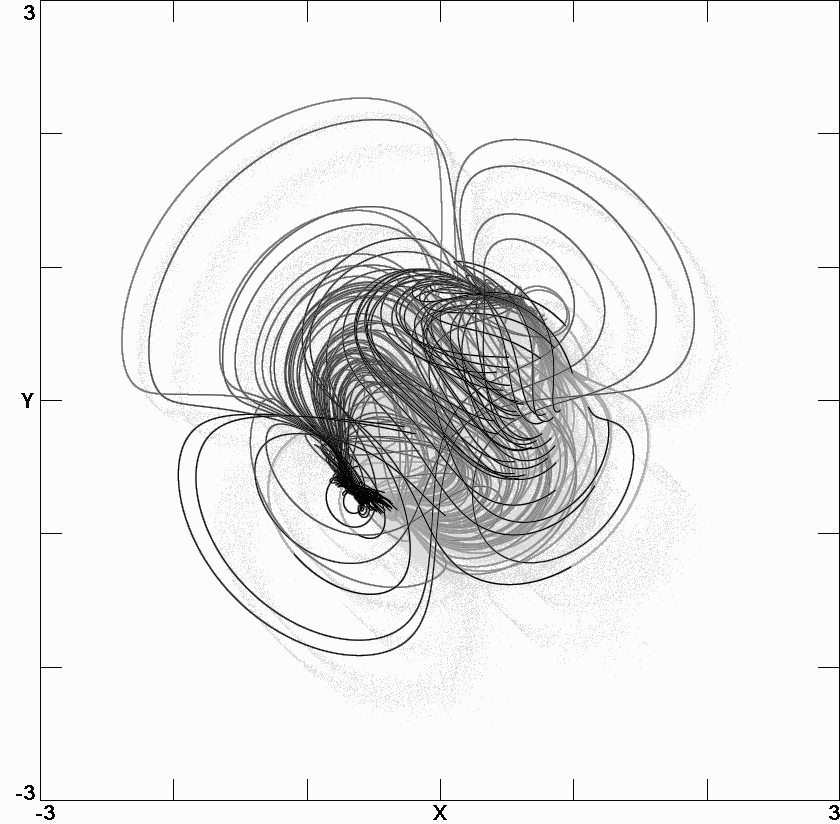
Fig. 8