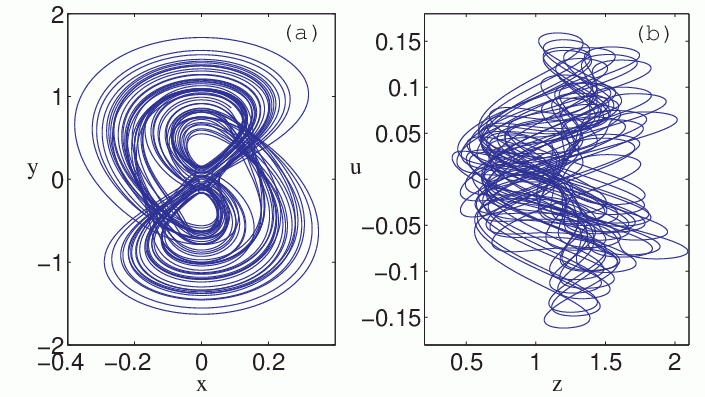
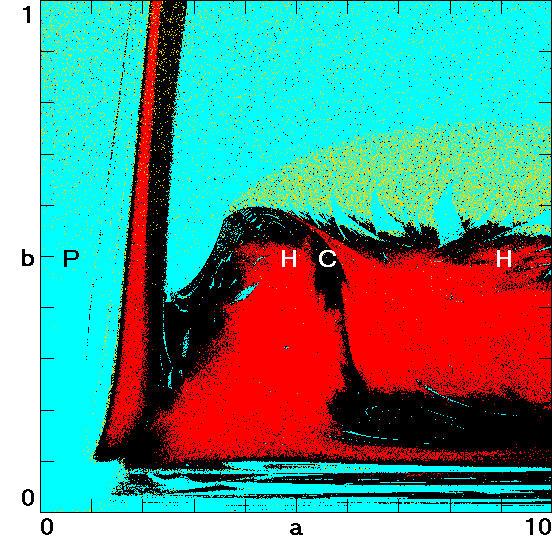
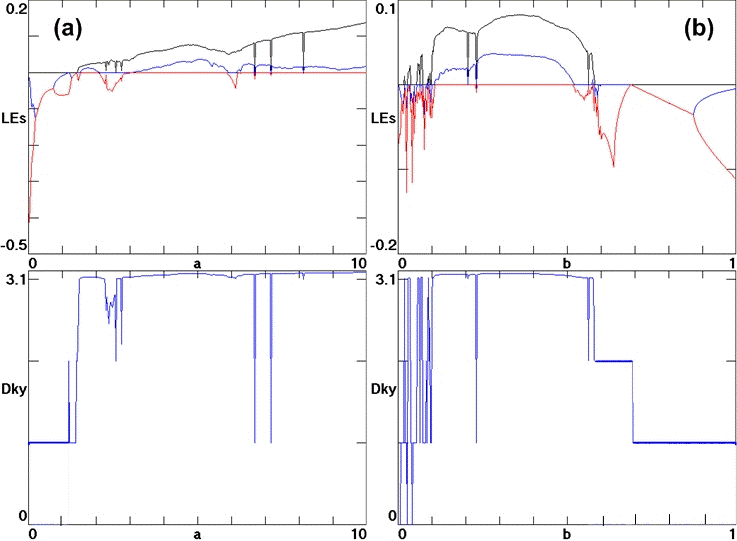
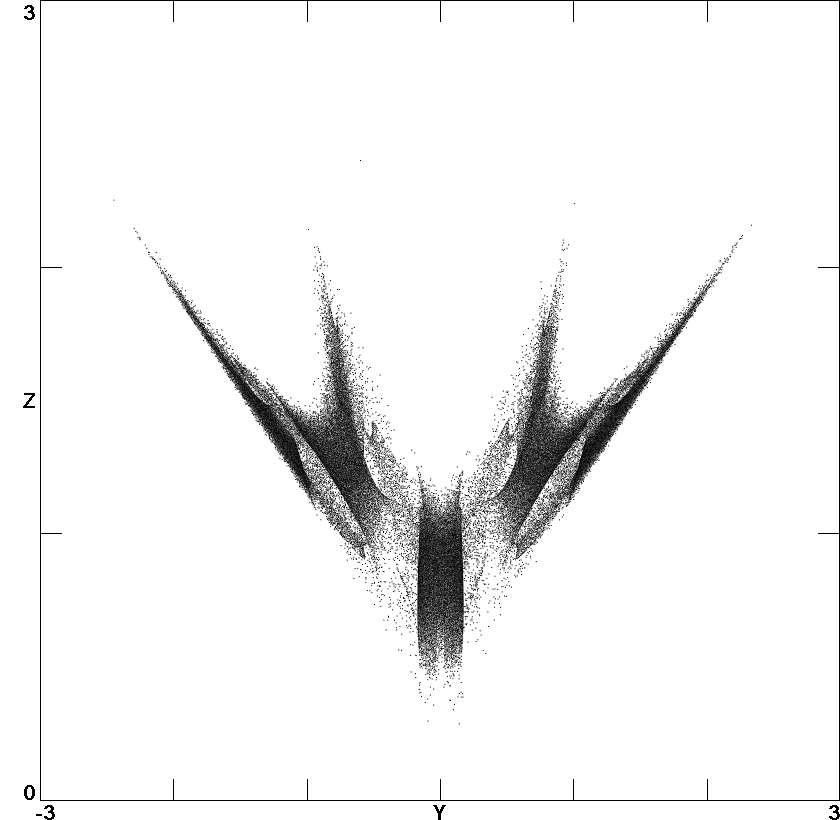Bistability in a Hyperchaotic System with a Line Equilibrium
Chunbiao Li
a, J.C.Sprott
b, Wesley Thio
c
aSchool of Information Science and
Engineering, Southeast University 210096, Nanjing, China
bDepartment of Physics, University of
Wisconsin-Madison 53706, Madison, WI, USA
cDepartment of Electrical and Computer
Engineering, The Ohio State University 43210, Columbus, OH, USA
Received October 26, 2013
A hyperchaotic system with an infinite line of
equilibrium points is described. A criterion is proposed for
quantifying the hyperchaos, and the position in the
three-dimensional parameter space where the hyperchaos is
largest is determined. In the vicinity of this point, different
dynamics are observed including periodicity, quasi-periodicity,
chaos, and hyperchaos. Under some conditions, the system has a
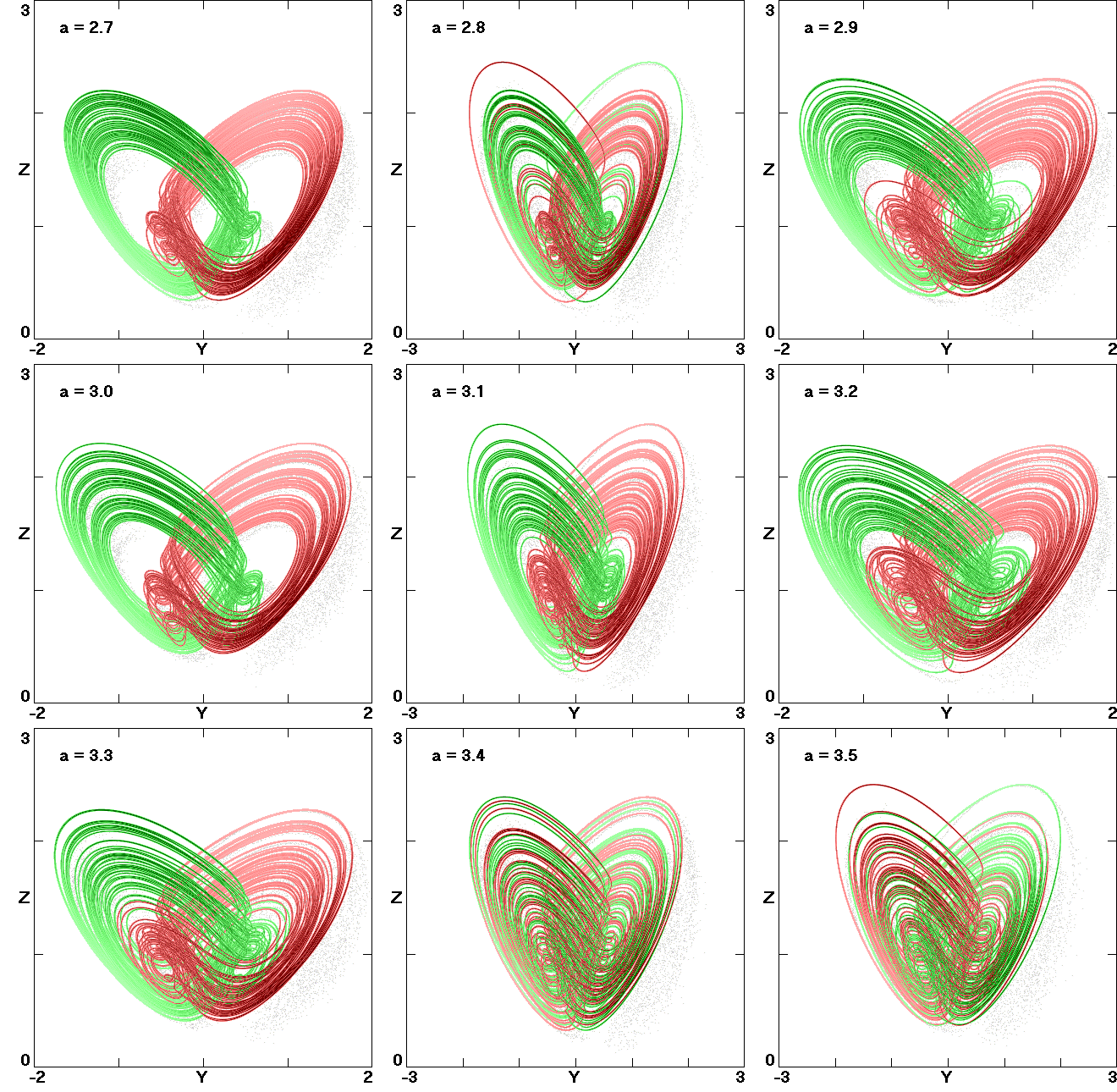
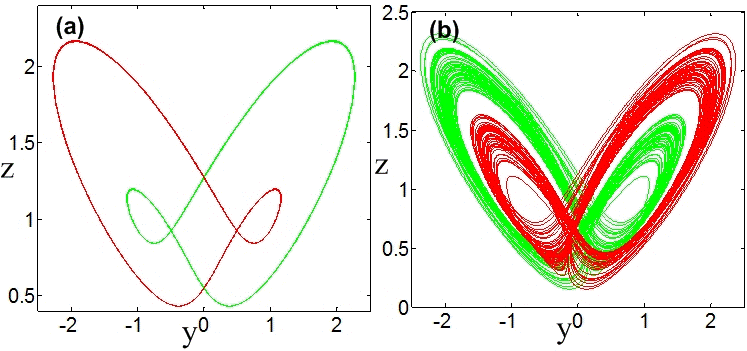
unique bistable behavior, characterized by a symmetric pair of
coexisting limit cycles that undergo period doubling, forming a
symmetric pair of strange attractors that merge into a single
symmetric chaotic attractor that then becomes hyperchaotic. The
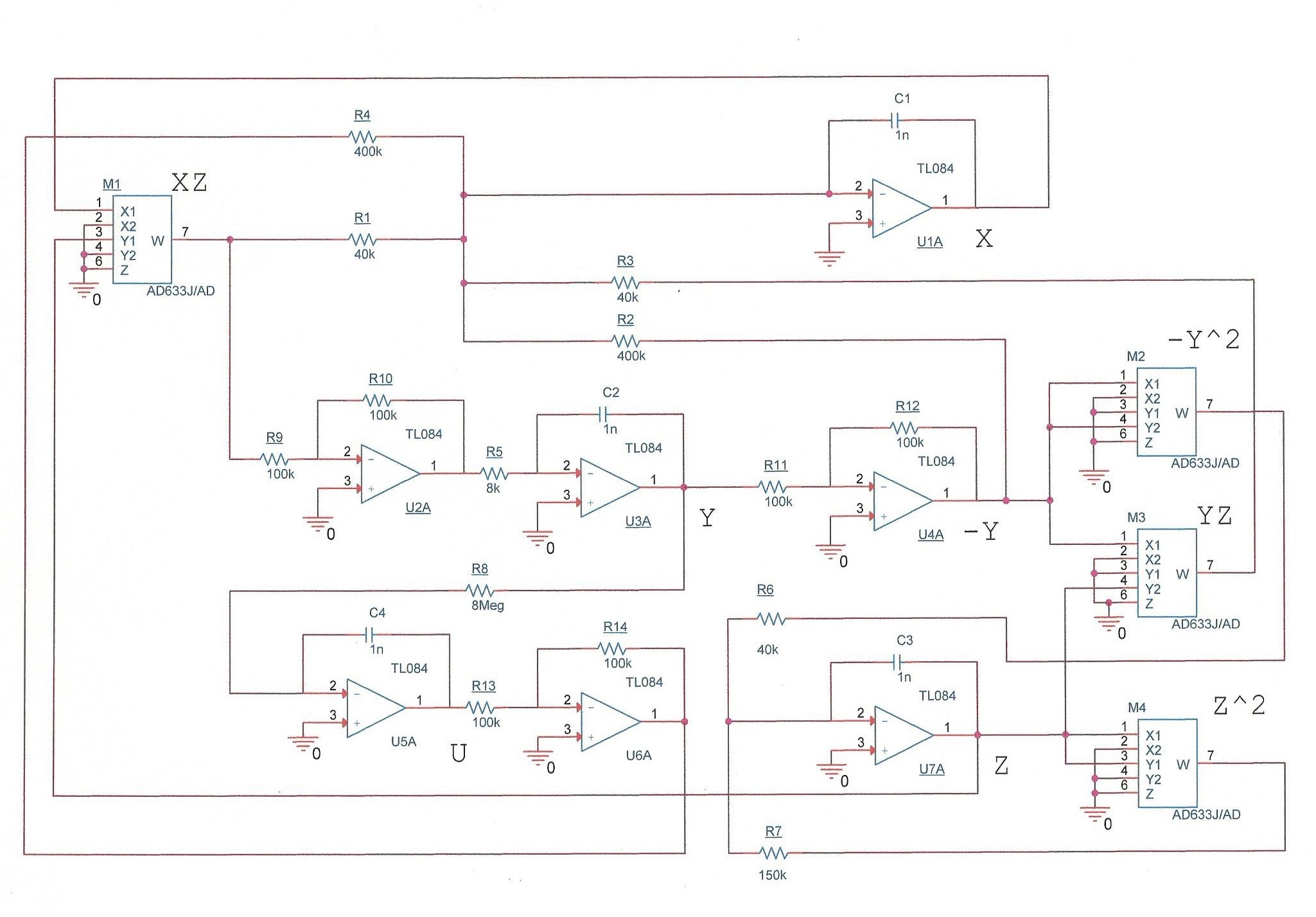
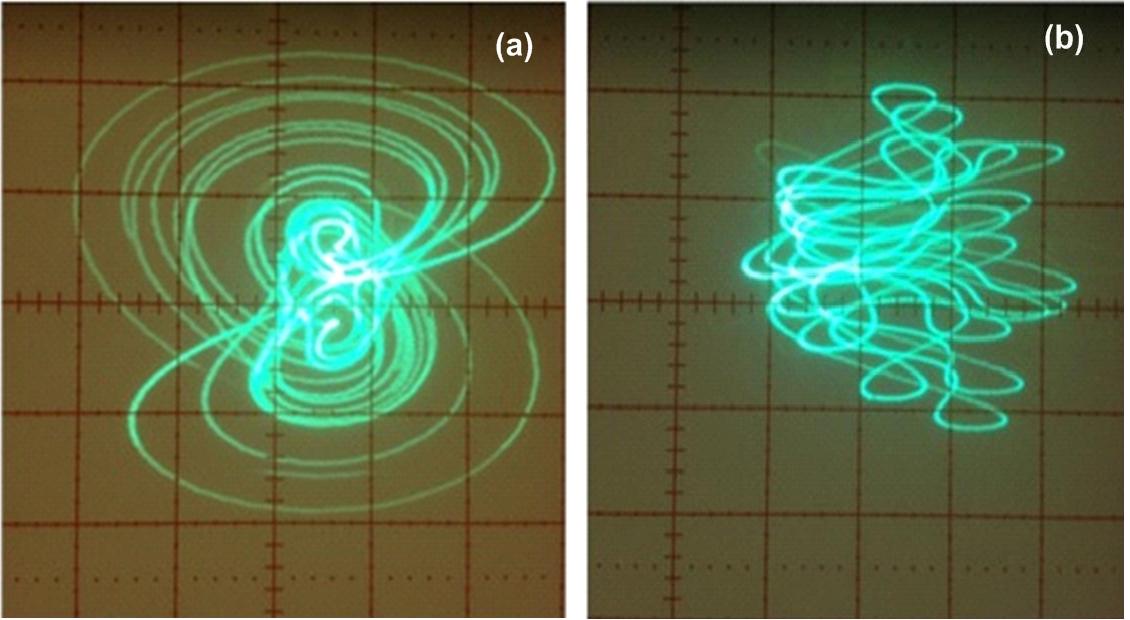
system was implemented as an electronic circuit whose behavior
confirms the numerical predictions.