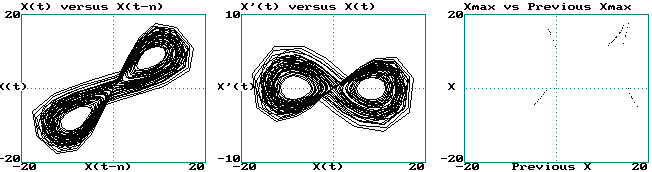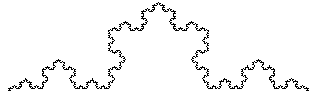Calculation of Fractal Dimension

Comments on Homework #10 (Time-Delay Reconstruction)

• Optimum n is about 2 (delay of 2 x 0.05 = 0.1 seconds)
• This is about equal to autocorrelation time (0.3 seconds) / D_E (3)
• It's very hard to see fractal structure in return map (D ~ 1.05)
• Your graphs should look as follows:

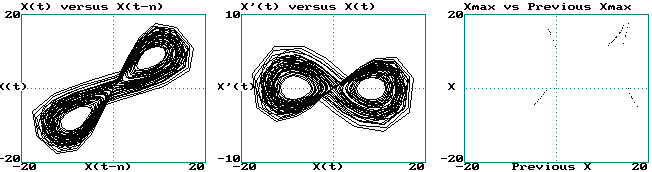
Review (last week) - Fractals

• Nonlinear prediction
• methods usually apply in state space
• methods can also remove some noise
• Can be used to produce an arbitrarily long time series
• Gives an accurate answer to an approximate model
• Lyapunov exponent of experimental data
• Getting the LE from experimental data is much more difficult (canned routines are recommended - See Wolf)
• Finding a value for LE may not be very useful
• Noise and chaos both have positive LEs (LE = infinity for white noise)
• Quasi-linear dynamics have zero LE, but there are better ways to detect it (look for discrete power spectrum)
• Hurst exponent (omitted)
• Deviation from starting point:  DX_rms = N^H
• Hence H is slope of log(DX_rms) versus N (or t)
• One convention is for white noise to have H = 0
• And brown noise (1/f ²) to have H = 0.5
• With this convention, H = a/4 for 1/f ^a noise
• Hurst exponent has same information as power law coefficient

Capacity Dimension

• The most direct indication of chaos is a strange attractor
• Strange attractors will generally have a low, non-integer dimension
• There are many ways to define and calculate the dimension
• We already encountered the Kaplan-Yorke dimension, but it requires knowledge of all the Lyapunov exponents
• Most calculations depend on the fact that amount of "stuff" M scales as d^D
• Hence D = d log(M) / d log(d)  [i.e., D is the slope of log(M) versus log(d)]
• One example is the capacity dimension (D₀)
• Closely related to the Hausdorf dimension or "cover dimension"
• Consider data representing a line and a surface embedded in 2-D
• The number of squares N of size d required to cover the line (1-D) is proportional to 1/d
• The number of squares N of size d required to cover the surface (2-D) is proportional to 1/d²
• The number of squares N of size d required to cover a fractal (dimension D₀) is proportional to 1/d^D0
• Hence the fractal dimension is given by  D₀ = d log(N) / d log(1/d)
• This is equivalent to  D₀ = -d log(N) / d log(d)
• Plot log(N) versus log(d) and take the (negative) slope to get D₀
• More typically D₀ is calculated using a grid of fixed squares
• Example (2000 data points from Hénon map with D_E = 2)
• This derivative should be taken in the limit d --> 0
• The idea can be generalized to D_E > 2 using (hyper)cubes
• Many data points are required to get a good result
• The number required increases exponentially with D₀
• If 10 points are needed to define a line (1-D),

then 100 points are needed to define a surface (2-D),
and 1000 points are needed to define a volume (3-D), etc.

Examples of Fractals

• There are many other ways to make fractals besides chaotic dynamics
• They are worthy of study in their own right
• They provide a new way of viewing the world
• Fractal slide show (another "lecture within a lecture")
• Nature's Fractals
• Snowflake
• Cantor set
• Cantor curtains
• Devil's staircase
• Hilbert curve
• Von Koch island
• Flat Fournier universe
• Weierstrass function  ( x(t) = S[cos(2ⁿt) / 2^(2-D)n] )
• Fractal word
• Sierpinski triangle
• Sierpinski carpet
• Cantor square
• Cantor maze
• Twin dragon
• Julia dendrite  (Z_n+1 = Z_n² + i)
• Fractal fern
• Maple leaf
• Peitgen tree
• Fractal tree
• Diffusion-limited aggregation
• Iterated function systems
• Cellular automata
• Game of life
• Strange attractors
• Mandelbrot set  (Z_n+1 = Z_n² + C)
• Some of these cases will be studied more in the next few weeks
• Some ways to produce fractals by computer:
• Chaotic dynamical orbits (strange attractors)
• Recursive programming
• Iterated function systems (the chaos game)
• Infinite mathematical sums (Weierstrass function, etc.)
• Boundaries of basins of attraction
• Escape-time plots (Mandelbrot, Julia sets, etc.)
• Random walks (diffusion)
• Diffusion limited aggregation
• Cellular automata (game of life, etc.)
• Percolation (fluid seeping through porous medium)
• Self-organized criticality (avalanches in sand piles)

Similarity Dimension

• Easy to calculate dimension for exactly self-similar fractals
• Example #1  (Sierpinski carpet):
• 
• Consists of 9 squares in a 3 x 3 array
• Eight squares are self-similar squares and one is empty
• Each time the linear scale is increased 3 x, the "stuff" increases 8 times

Hence, D = log(8) / log(3) = 1.892789261...
• Note: Any base can be used for log since it involves a ratio
• Example #2  (Koch curve):
• 
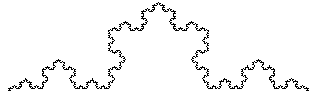
• Consists of 4 line segments:  _/\_
• Each factor of 3 increase in length adds 4 x the "stuff"

Hence, D = log(4) / log(3) = 1.261859507...
• Example #3  (Triadic Cantor set):
• 
• Consists of three line segments  ^{_____ _____ _____}
• Two segments are self similar and one is empty
• Each factor of 3 increase in length adds 2 x the "stuff"
• Hence, D = log(2) / log(3) = 0.630929753

Correlation Dimension

• Capacity dimension does not give accurate results for experimental data
• Similarity dimension is hard to apply to experimental data
• The best method is the (two-point) correlation dimension (D₂)
• This method opened the floodgates for identifying chaos in experiments
• Next homework asks you to calculate D₂ for the Hénon map
• Original (Grassberger and Procaccia) paper included with HW #12
• Illustration for 1-D and 2-D data embedded in 2-D
• Procedure for calculating the correlation dimension:
• Choose an appropriate embedding dimension D_E
• Choose a small value of r (say 0.001 x size of attractor)
• Count the pairs of points C(r) with Dr < r
• Dr = [(X_i - X_j)² + (X_i-1 - X_j-1)² + ...]^1/2
• Note: this requires a double sum (i, j) ==> 10⁶ calculations for 1000 data points
• Actually, this double counts; can sum j from i+1 to N
• In any case, don't include the point with i = j
• Increase r by some factor (say 2)
• Repeat count of pairs with Dr < r
• Graph log C(r) versus log r (can use any base)
• Fit curve to a straight line
• Slope of that line is D₂
• Think of C(r) as the probability that 2 random points on the attractor are separated by < r
• Example:  C(r) versus r for Hénon map with N = 1000 and D_E = 2
• Result:  D₂ = 1.223 ± 0.097
• Compare:  D_GP = 1.21 ± 0.01 (Original paper, N = 15,000)
• Compare:  D_KY = 1.2583  (from Lyapunov exponents)
• Compare:  D₀ = 1.26  (published result for capacity dimension)
• See also my calculations with N = 3 x 10⁶
• Generally  D₂ < D_KY< D₀  (but they are often close)
• Sometimes the convergence is very slow as r --> 0
• Tips for speeding up the calculation (in order of difficulty):
• Avoid double counting by summing j from i+1 to N
• Collect all the r values at once by binning the values of Dr
• Avoid taking square roots by binning Dr² and using log x² = 2 log x
• Avoid calculating log by using exponent of floating point variable
• Collect data for all embeddings at once
• Sort the data first so you can quit testing when Dr exceeds r
• Can also use other norms, but accuracy suffers
• Number of data points needed to get valid correlation dimension
• Need a range of r values over which slope is constant (scaling region)
• Limited at large r by the size of the attractor (D₂ = 0 for r > attractor size)
• Limited at small r by statistics (need many points in each bin)
• Various criteria, all predict N increases exponentially with D₂
• Tsonis criterion:  N ~ 10 ^{2 + 0.4D}  (D to use is probably D₂)

D	N
1	250
2	630
3	1600
4	4000
5	10,000
6	25,000
7	63,000
8	158,000
9	400,000
10	1,000,000